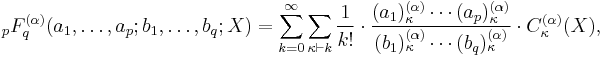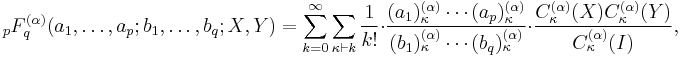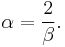Hypergeometric function of a matrix argument

In mathematics, the hypergeometric function of a matrix argument is a generalization of the classical hypergeometric series. It is a function defined by an infinite summation which can be used to evaluate certain multivariate integrals.

Hypergeometric functions of a matrix argument have applications in random matrix theory. For example, the distributions of the extreme eigenvalues of random matrices are often expressed in terms of the hypergeometric function of a matrix argument.

1 Definition
2 Two matrix arguments
3 Not a typical function of a matrix argument
4 The parameter
5 References
6 External links

Definition

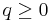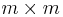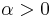Let $p\ge 0$ and $q\ge 0$ be integers, and let $X$ be an $m\times m$ complex symmetric matrix. Then the hypergeometric function of a matrix argument $X$ and parameter $\alpha>0$ is defined as

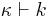$_pF_q^{(\alpha )}(a_1,\ldots,a_p; b_1,\ldots,b_q;X) = \sum_{k=0}^\infty\sum_{\kappa\vdash k} \frac{1}{k!}\cdot \frac{(a_1)^{(\alpha )}_\kappa\cdots(a_p)_\kappa^{(\alpha )}} {(b_1)_\kappa^{(\alpha )}\cdots(b_q)_\kappa^{(\alpha )}} \cdot C_\kappa^{(\alpha )}(X),$

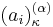where $\kappa\vdash k$ means $\kappa$ is a partition of $k$ , $(a_i)^{(\alpha )}_{\kappa}$ is the Generalized Pochhammer symbol, and 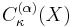$C_\kappa^{(\alpha )}(X)$ is the ``C" normalization of the Jack function.

Two matrix arguments

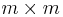If $X$ and $Y$ are two $m\times m$ complex symmetric matrices, then the hypergeometric function of two matrix arguments is defined as:

$_pF_q^{(\alpha )}(a_1,\ldots,a_p; b_1,\ldots,b_q;X,Y) = \sum_{k=0}^\infty\sum_{\kappa\vdash k} \frac{1}{k!}\cdot \frac{(a_1)^{(\alpha )}_\kappa\cdots(a_p)_\kappa^{(\alpha )}} {(b_1)_\kappa^{(\alpha )}\cdots(b_q)_\kappa^{(\alpha )}} \cdot \frac{C_\kappa^{(\alpha )}(X) C_\kappa^{(\alpha )}(Y) }{C_\kappa^{(\alpha )}(I)},$

where $I$ is the identity matrix of size $m$ .

Not a typical function of a matrix argument

Unlike other functions of matrix argument, such as the matrix exponential, which are matrix-valued, the hypergeometric function of (one or two) matrix arguments is scalar-valued.

The parameter $\alpha$

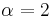In many publications the parameter $\alpha$ is omitted. Also, in different publications different values of $\alpha$ are being implicitly assumed. For example, in the theory of real random matrices (see, e.g., Muirhead, 1984), $\alpha=2$ whereas in other settings (e.g., in the complex case--see Gross and Richards, 1989), 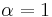$\alpha=1$ . To make matters worse, in random matrix theory researchers tend to prefer a parameter called $\beta$ instead of $\alpha$ which is used in combinatorics.

The thing to remember is that

$\alpha=\frac{2}{\beta}.$

Care should be exercised as to whether a particular text is using a parameter $\alpha$ or $\beta$ and which the particular value of that parameter is.

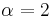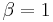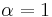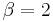Typically, in settings involving real random matrices, $\alpha=2$ and thus $\beta=1$ . In settings involving complex random matrices, one has $\alpha=1$ and $\beta=2$ .

References

K. I. Gross and D. St. P. Richards, "Total positivity, spherical series, and hypergeometric functions of matrix argument", J. Approx. Theory, 59, no. 2, 224–246, 1989.

J. Kaneko, "Selberg Integrals and hypergeometric functions associated with Jack polynomials", SIAM Journal on Mathematical Analysis, 24, no. 4, 1086-1110, 1993.

Plamen Koev and Alan Edelman, "The efficient evaluation of the hypergeometric function of a matrix argument", Mathematics of Computation, 75, no. 254, 833-846, 2006.

Robb Muirhead, Aspects of Multivariate Statistical Theory, John Wiley & Sons, Inc., New York, 1984.

External links

Software for computing the hypergeometric function of a matrix argument by Plamen Koev.